- Published on
Semi Supervised Domain Adaptation과 Noisy Label Learning(CVPR2023)
- Authors

- Name
- Minkyoung Shin
Semi-Supervised Domain Adaptation with Source Label Adaptation
Semi Supervised Domain Adaptation 의 전제조건 : 보지 못한 target data와 몇장의 라벨링된 데이터를 다량의 target domain 과 비슷한 결의 source data를 사용해서 classification 하는 작업이다.
기존의 작업들은 소스 데이터에 noise 가 껴서 label 이 잘못되어있거나, target data와 match 가 안된다는 문제점을 지니고 있다 → 따라서 본 논문에서는 source data를 target data 로 adapt하는 방식을 제안한다.
또한 target data 관점에서 adaptation 하는데 잘 맞지 않는 source data의 noisy 한 소스 데이터를 제거함으로써, 타겟 데이터에 잘 맞으면서 잘못된 라벨링을 가려낼 수 있는 방식 또한 제안하였다.
Method
기존 semi supervised 방식은 단순히 소스 데이터와 타겟 데이터간 cross entropy loss 를 걸어서 domain adaptation 을 진행하였으나, 이 방식같은 경우에는 domain shift 문제가 발생한다. (타겟과 소스간 차이가 너무 커서 adaptation 이 잘 안되는 것)
또한 이 문제 해결하기 위해, 라벨링 안된 데이터셋에다가 수도 라벨링을 하거나, entropy minimization 을 진행하거나, comsistency regularization 등을 진행한다.
→ 근데 이런것도 타겟 데이터가 어느정도 소스 데이터와 semantic하게 비슷해야한다는 것을 전제하므로, 한계가 명확하게 존재한다.
단순히 기존 방식으로만 접근을 하면 domain adaptation 당시 target 데이터가 잘못된 source label 과 비슷해질 염려가 있다.
그니까 타겟 데이터 입장에서는 노이즈가 낀 소스 데이터(= ideal label)가 될 수 있다는 점(실제로 노이즈가 낀게 아니라, target 에 잘 맞지 않는 source data라는 뜻)
이에 대한 명칭을 Nosiy label learning 이라고 부름
→ 본 논문의 궁극적인 목표는 소스 데이터를 얼만큼 잘 ideal 한 target space에 맞게 adapted label 로 맞추도록 학습할 수 있느냐가 되는 것이다.
NLL 문제를 해결하려고 하는 다양한 논문들이 있었는데, 이런 방법들이 직접적으로 SSDA를 해결하는 것은 아니였기 때문에, 이 둘의 네트워크 간 연결성을 풀고자 하였다.
일단 noisy 한 소스 데이터를 ideal 하게 만들기 위해서, DA방식을 NLL 처럼 해결하려고 했는데,
- 기존에 noisy 가 낀 소스 데이터를 ideal 한 noisy 낀 소스 데이터로 보고 한번 거르는 작업을 진행
- 근데 이런식으로 거르면 결국에 걸러진 데이터가 noisy 낀 데이터 (기존) 것과 비슷해질 수 밖에 없다. source data인 자기자신만 보고 update를 하기 때문에 (이게 label correction with self-prediction이라고 함)
- 따라서 target domain 관점에서 ideal label 을 만드는 작업을 채택하였다. ( 가 바로 그 모델임)
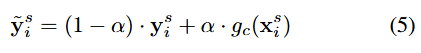
그렇다면 이 라벨의 확률분포 결과를 내뱉는 모델 를 어떤 방식으로 정의할 것인가?
Protonet with Pseudo Centers
바로 이 Protonet을 사용하는데,
이 모델은 Protonet with Pseudo Centers 를 사용하여 few shot labeling 된 타겟 이미지가 있었을 때 overfitting 되는 문제를 해결하고자 하였다.

는 Target domain의 unlabeled data로부터 만들어진 클래스별 중심(Prototype)
코드로 확인해보면,
t_pred, t_feat = prediction(t_loader, model)
label = t_pred.argmax(dim=1)
center = [t_feat[label == i].mean(dim=0) for i in range(num_classes)]
- 여기서
t_loader는 target domain의 validation or unlabeled test loader - 따라서
self.center는 target domain feature space 기준의 중심
Centers 는 어떻게 구하는 것인가?
center를 잡는 과정은 unlabeled target data에 대해서 수도 라벨(pseudo label)을 기반으로 잡는데, 정답은 모르지만, model의 예측 결과를 신뢰해서 pseudo label로 취급하는 방식이라고 보면 된다. source label 의 정답 라벨이 아니라, 모델이 현재까지 학습한 결과를 기반으로 만든 pseudo prototype이라고 생각하면 된다.
결국 이 center가 target 도메인에 맞게 source label을 adaptation 하기 위한 reference 역할을 하는 것!

입력 x는 일반적으로 source domain의 feature (학습용 데이터)로, 이 x와 target 도메인의 중심 (self.center) 간 거리를 바탕으로 soft label 생성한다.
dist = torch.cdist(x, self.center)
soft_label = F.softmax(-dist * T, dim=1)
이 soft label은 "이 source feature가 target domain 상에서 어떤 class prototype에 가까운가?"
라는 target-aligned 예측 확률을 나타낸다.
즉, self.center는 target feature 공간에서 각 클래스의 평균 벡터 (prototype)가 되는거고, soft label(prototype network 의 output) 은 클래스별 확률을 가지는 것!

최종 소스에 대한 업데이트 되는 라벨 식을 보면, 알파 값을 통해 hard label(원핫인코딩) 과 soft label(확률분포)간의 비율을 조정해주고, prototype network 는 unlabeled 된 target data 를 self.center로 두어 source data 가 들어갔을 때 뱉는 soft label 이라고 보면 된다.
| 파라미터 | 역할 | 값 | 학습에 미치는 영향 |
|---|---|---|---|
--alpha | SLA 손실에서 hard label과 soft label의 비율 | 0.3 | hard label:soft label = 0.7:0.3 → soft label은 보조적인 힌트 역할 |
--update_interval | prototype(center) 업데이트 주기 | 500 | 모델이 변화함에 따라 target prototype을 얼마나 자주 새로 계산할지 |
--warmup | SLA 시작 시점 | 50000 | 5만 스텝 전까지는 일반 CE loss만 사용 → 안정화된 후 soft label 사용 시작 |
--T | prototype soft label의 temperature | 0.6 | 낮을수록 더 "확신 있는" soft label → sharpened 분포로 학습 강제함 |
MME+ SLA
SLA 같은 경우에는 모듈로써 네트워크 통으로 제안하는게 아니라, 기존 SOTA 모델에 붙여서 사용했었을 때 adaptation 성능이 올라간다는 것을 제안하였는데, 이 SOTA모델로 MME와 CDAC를 대표적으로 사용하였다.
MME는Minimum Entropy for Semi-supervised Domain Adaptation의 약자로, domain adaptation에서 target 도메인에 label이 없을 때에도 의미 있는 피드백을 주는 기법이다. (즉 unlabled target에 대한 loss 를 제안한 논문)
이 개념은 2020년 CVPR 논문인 "Minimum Class Confusion for Domain Adaptation" 및 "Unsupervised Domain Adaptation by Minimizing Conditional Entropy" 등의 영향을 받았다.
기존 domain adaptation 에서는 source domain에는 label이 있지만, target domain에는 label이 없다는 전제 조건과, 일반적으로 target 샘플은 loss 계산에 사용할 수 없기 떄문에, 학습이 어렵다는 단점이 2020년도에는 존재했었다. MME 는 이에 대해 target domain 데이터에 대해서도 low entropy 예측을 하도록 모델을 구성하자는게 메인으로, MME Loss를
MME는 target 입력 에 대해 다음을 최소화하도록 학습된다.
def mme_loss(self, _, x, lamda=0.1):
out = self.forward(x, reverse=True) # reverse = gradient reversal
out = F.softmax(out, dim=1) # 확률 분포화
return lamda * torch.mean(torch.sum(out * (torch.log(out + 1e-10)), dim=1))
- out: target sample에 대한 softmax 결과
- torch.sum(out * log(out)): entropy
- lamda: loss에 적용되는 가중치
이런식으로 loss를 구성하게 되면 unlabled된 target data에도 labeling 이 하나에 클래스에 confident 하게 확률 분포가 구성되는 방식으로 학습되게 되므로, 타겟 데이터에 대해 예측 분포의 엔트로피를 줄이도록 학습되는 방식이라고 보면 된다.
즉, target 예측의 entropy를 줄이는 것 → 결과적으로 더 confident한 결정 경계를 유도하는 것 !
Gradient reversal layer (GRL) 을 통한 min-max 구조 학습
MME에서는 classifier 입장에서는 entropy 를 최대화하는 방식으로, feature extractor는 entropy를 최소화하는 방식으로 학습이 되어야 하는데, (classifier의 entropy를 줄이면 classifier가 너무 confident 해져서 모델이 overfitting 날 확률이 있기 때문에, classifier는 entropy 를 최대화로 만들고, feature extractor는 이를 이겨내서 entropy 를 줄이도록 학습한다)
이 구조로 학습하게 되면 domain-invariant 하면서도 class-discriminative한 피처를 만드는데 이점을 지닌다.
🧠 참고:
reverse=True → Gradient Reversal Layer 사용 (DANN과 동일한 기법)
Gradient Reversal Layer(GRL)는 도메인 적응에서 사용되는 특수한 연산으로, 순전파에서는 입력을 그대로 통과시키지만 역전파 시에는 gradient의 부호를 반전시켜 모델이 도메인 분류기를 속이도록 학습하게 만든다. 이를 통해 feature extractor가 source와 target 도메인을 구분할 수 없도록 일반화된 특징을 추출하게 하며, adversarial 학습 구조에서 핵심적인 역할을 수행한다.
CDAC + SLA
CDAC는 "Class-aware Domain Alignment with Consistency for Semi-supervised Domain Adaptation"의 약자로, MME의 entropy minimization 개념을 확장하여, 클래스 중심(class-aware)과 일관성(consistency)까지 통합한 방식이다.
CDAC는 크게 3가지 손실 함수로 구성된다 :
| 구성 요소 | 손실 함수 | 목적 |
|---|---|---|
| ① Adversarial Alignment | advbce_unlabeled | unlabeled target 데이터 군집화 |
| ② Pseudo Label Supervision | pl_loss | confident pseudo-label 예측을 정답처럼 학습 |
| ③ Consistency Regularization | con_loss | 같은 입력의 augmentation 간 예측 일관성 유지 |
CDAC 코드 분석: cdac_loss
def cdac_loss(self, step, x, x1, x2):
w_cons = 30 * sigmoid_rampup(step, 2000) # consistency 점진적 증가
x: unlabeled target 원본x1,x2: 동일한x에 대한 augmentation (ex. strong, weak)step: 현재 iteration (일정 step 후에 consistency를 점차 증가)
세가지 로스를 각각 뜯어보면,
① Adversarial Alignment Loss (aac_loss)
f = self.f(x)
f1 = self.f(x1)
out = self.c(f, reverse=True)
out1 = self.c(f1, reverse=True)
prob, prob1 = F.softmax(out, dim=1), F.softmax(out1, dim=1)
aac_loss = advbce_unlabeled(
target=None, f=f, prob=prob, prob1=prob1, bce=self.bce
)
def advbce_unlabeled(target, f, prob, prob1, bce):
"""
Construct adversarial adaptive clustering loss.
Args:
target: (optional, unused here) ground-truth label or pseudo-label
f: feature vectors from original input x (shape: [B, D])
prob: softmax outputs of x (shape: [B, C])
prob1: softmax outputs of x1 (augmented) (shape: [B, C])
bce: a binary cross-entropy-like loss module (BCE_softlabels)
"""
target_ulb = pairwise_target(f, target) # shape: [B * B]
prob_bottleneck_row, _ = PairEnum2D(prob) # shape: [B * B, C]
_, prob_bottleneck_col = PairEnum2D(prob1) # shape: [B * B, C]
adv_bce_loss = -bce(prob_bottleneck_row, prob_bottleneck_col, target_ulb)
return adv_bce_loss
reverse=True: Gradient Reversal Layer (GRL)를 거쳐서 domain classifier를 속이도록 학습advbce_unlabeled: 도메인 불변 feature 유도를 위한 adversarial binary cross entropy 손실
→ GRL + Adversarial BCE = MME처럼 작동, 그러나 두 가지 입력(f, f1)으로 정밀화한 방식이라고 보면 된다.
② Pseudo Label Loss (pl_loss)
out = self.c(f) # x의 일반 분류 예측
out2 = self.c(self.f(x2)) # x2 = augmented x
prob = F.softmax(out, dim=1)
mp, pl = torch.max(prob.detach(), dim=1)
mask = mp.ge(0.95).float() # confidence가 95% 이상일 때만 사용
pl_loss = (F.cross_entropy(out2, pl, reduction="none") * mask).mean()
pl: confident한 pseudo-labelmask: 특정 라벨이라고 confident score 가 높은 샘플만 손실에 포함out2: augmented view의 예측이 pseudo-label과 맞도록 유도
→ Self-training 방식과 유사하나, confident한 예측은 정답처럼 학습한다.
③ Consistency Loss (con_loss)
con_loss = F.mse_loss(prob1, prob2)
prob1:x1에 대한 softmaxprob2:x2에 대한 softmax- 같은 샘플(x)의 서로 다른 augmentation 간에 예측 일관성을 유지하도록 제약을 거는 loss라고 보면 된다.
최종 CDAC 손실 함수
return aac_loss + pl_loss + w_cons * con_loss
- 세 가지 손실을 더한다.
w_cons: consistency loss는 초기에는 무시하고, 학습이 안정되면 점차 증가
이렇게 각각 MME, CDAC에서 제안한 Loss에 SLA loss를 추가하여 성능 향상을 입증한 것이다.
Experiment & Results
직접 실험을 통해 MME + SLA 조합이 기존 방식 대비 얼마나 성능 향상을 가져오는지 검증해보았다.
실험은 DomainNet과 같은 벤치마크 데이터셋을 기반으로 진행되었으며, target domain에만 소량의 라벨링 데이터를 제공하는 semi-supervised setting에서 수행되었다. (코드 실험 및 ResNet 50으로 바꿔서 실험했었을 때 결과를 확인해보고 싶었다.)
아래는 SLA loss 적용 전후의 주요 성능 지표 비교이다:

논문 수치보다 높거나 비슷하게 나온 결과를 확인해 볼 수 있었다.
ResNet50으로 바꿔서 실험한 결과도 진행해보았는데,

확실히 성능 향상 효과가 있었다. 아마 이전 논문들과의 fair한 비교를 위해서 ResNet34를 선택했을 듯.
추가적으로 정리한 내용들
1. Hard Label vs. Soft Label
| 구분 | 정의 | 예시 (C=3) | 설명 |
|---|---|---|---|
| Hard Label | 정답 클래스만 1, 나머지는 0 | [0, 1, 0] | 클래스 1이 정답 |
| Soft Label | 모델 출력의 확률 분포 | [0.2, 0.7, 0.1] | 모델이 예측한 클래스 확률 분포 |
2. 왜 "soft-label"을 쓸까?
특히 semi-supervised learning, domain adaptation, knowledge distillation, SLA (Soft Label Adaptation) 같은 상황에서는:
- Unlabeled 데이터에 대해 "정답"이 없음
- 따라서 해당 이미지의 예측값을 신뢰도 있게 추정하여 pseudo-label로 사용
- 이때 확률 분포 전체를 활용하는 것이 hard label보다 더 유연하고 정보량이 많음
logits = model(x) # shape: (batch, num_classes)
soft_label = F.softmax(logits / T, dim=1) # softmax with temperature
T(temperature) ↑면 분포가 더 flat (부드럽고, 불확실성 반영)- 이
soft_label은 cross-entropy에서 target으로 쓰일 수 있음!:
loss = F.kl_div(F.log_softmax(pred, dim=1), soft_label, reduction='batchmean')
더 자세한 내용은, 본 논문을 참고하면 된다 ! :
📄 Read the paper on arXiv